티스토리 뷰
<목차>
1. 데이터 확인
1-1. 데이터 소개
- 레드 와인의 물리 화학적 특징과 퀄리티 점수를 보여주는 CSV파일 데이터

1-2. 데이터 구조 분석
- 데이터를 불러온다.
wine<-read.csv("wineQualityReds.csv")
- 데이터의 structure를 확인한다.
str(wine)'data.frame': 1599 obs. of 13 variables:
$ X : int 1 2 3 4 5 6 7 8 9 10 ...
$ fixed.acidity : num 7.4 7.8 7.8 11.2 7.4 7.4 7.9 7.3 7.8 7.5 ...
$ volatile.acidity : num 0.7 0.88 0.76 0.28 0.7 0.66 0.6 0.65 0.58 0.5 ...
$ citric.acid : num 0 0 0.04 0.56 0 0 0.06 0 0.02 0.36 ...
$ residual.sugar : num 1.9 2.6 2.3 1.9 1.9 1.8 1.6 1.2 2 6.1 ...
$ chlorides : num 0.076 0.098 0.092 0.075 0.076 0.075 0.069 0.065 0.073 0.071 ...
$ free.sulfur.dioxide : num 11 25 15 17 11 13 15 15 9 17 ...
$ total.sulfur.dioxide: num 34 67 54 60 34 40 59 21 18 102 ...
$ density : num 0.998 0.997 0.997 0.998 0.998 ...
$ pH : num 3.51 3.2 3.26 3.16 3.51 3.51 3.3 3.39 3.36 3.35 ...
$ sulphates : num 0.56 0.68 0.65 0.58 0.56 0.56 0.46 0.47 0.57 0.8 ...
$ alcohol : num 9.4 9.8 9.8 9.8 9.4 9.4 9.4 10 9.5 10.5 ...
$ quality : int 5 5 5 6 5 5 5 7 7 5 ...-> 13개의 변수와 1599개의 데이터를 가지고 있다.
-> 모든 변수가 연속형 변수임을 알 수 있다.
<변수 설명>
fixed.acidity(결합산) : 와인의 산도를 제어한다.
volatile.acidity(휘발산) : 와인의 향에 연관이 많다.
citric.acid(구연산) : 와인의 신선함을 유지시켜주는 역할을 하며, 산성화에 연관을 미친다.
residual.sugar(잔여 설탕) : 와인의 단맛을 올려준다.
chlorides(염소) : 와인의 짠맛과 신맛을 좌우하는 성분이다.
free.sulfur.dioxide / total.sulfur.dioxide / sulphates(황 화합물) : 특정 박테리아와 효모를 죽여 와인의 보관도를 높여준다.
density(밀도) : 바디의 높고 낮음을 표현하는 와인의 바디감을 의미한다.
pH(산성도) : 와인의 신맛의 정도를 나타낸다.
alcohol(알코올) : 와인에 단맛을 주며 바디감에 영향을 준다.
quality(퀄리티) : 결과적으로 다른 변수들을 이용하여 예측하려고 하는 변수로 와인의 퀄리티를 나타낸다.
2. 데이터 분석
2-1. 데이터 정제
- 필요 없는 X 변수를 제거해준다.
wine$X <- NULL
- N/A 결측치가 있는지 확인한다.
colSums(is.na(wine)) fixed.acidity volatile.acidity citric.acid residual.sugar
0 0 0 0
chlorides free.sulfur.dioxide total.sulfur.dioxide density
0 0 0 0
pH sulphates alcohol quality
0 0 0 0-> 결측치를 가지는 변수가 없는 깔끔한 데이터임을 알 수 있다.
- 예측해야하는 quility 변수가 연속형 변수이기때문에 이산형화 해주어야한다.
- quality 변수의 분포를 관찰해본다.
table(wine$quality)
3 4 5 6 7 8
10 53 681 638 199 18summary(wine$quality)
Min. 1st Qu. Median Mean 3rd Qu. Max.
3.000 5.000 6.000 5.636 6.000 8.000library(ggplot2)theme_set(theme_minimal())
ggplot(wine,aes(quality)) + geom_histogram(stat="count") +
xlab("Quality of white wines") + ylab("Number of white wines") + geom_bar(fill="pink")
-> 대부분의 와인들의 퀄리티 점수가 5-6임을 알 수 있다.
-> 점수가 7이상이면 꽤 괜찮은 와인이라고 판단할 수 있을 것 같다.
- rating 변수를 추가로 생성해준다.
- 점수가 7 이상일 경우 1("Good") / 점수가 7 미만일 경우 0("Not Good")
wine$rating<-ifelse(as.integer(wine$quality) > 6, "Good", "Not Good")table(wine$rating) 0 1
1382 217-> 217개의 데이터가 괜찮은 와인으로 분류되었다.
2-2. 탐색적 데이터 분석
- 변수 별로 도수분포표를 살펴본다.
summary(wine) fixed.acidity volatile.acidity citric.acid residual.sugar chlorides
Min. : 4.60 Min. :0.1200 Min. :0.000 Min. : 0.900 Min. :0.01200
1st Qu.: 7.10 1st Qu.:0.3900 1st Qu.:0.090 1st Qu.: 1.900 1st Qu.:0.07000
Median : 7.90 Median :0.5200 Median :0.260 Median : 2.200 Median :0.07900
Mean : 8.32 Mean :0.5278 Mean :0.271 Mean : 2.539 Mean :0.08747
3rd Qu.: 9.20 3rd Qu.:0.6400 3rd Qu.:0.420 3rd Qu.: 2.600 3rd Qu.:0.09000
Max. :15.90 Max. :1.5800 Max. :1.000 Max. :15.500 Max. :0.61100
free.sulfur.dioxide total.sulfur.dioxide density pH sulphates
Min. : 1.00 Min. : 6.00 Min. :0.9901 Min. :2.740 Min. :0.3300
1st Qu.: 7.00 1st Qu.: 22.00 1st Qu.:0.9956 1st Qu.:3.210 1st Qu.:0.5500
Median :14.00 Median : 38.00 Median :0.9968 Median :3.310 Median :0.6200
Mean :15.87 Mean : 46.47 Mean :0.9967 Mean :3.311 Mean :0.6581
3rd Qu.:21.00 3rd Qu.: 62.00 3rd Qu.:0.9978 3rd Qu.:3.400 3rd Qu.:0.7300
Max. :72.00 Max. :289.00 Max. :1.0037 Max. :4.010 Max. :2.0000
alcohol quality rating
Min. : 8.40 Min. :3.000 Min. :0.0000
1st Qu.: 9.50 1st Qu.:5.000 1st Qu.:0.0000
Median :10.20 Median :6.000 Median :0.0000
Mean :10.42 Mean :5.636 Mean :0.1357
3rd Qu.:11.10 3rd Qu.:6.000 3rd Qu.:0.0000
Max. :14.90 Max. :8.000 Max. :1.0000
- 변수 별로 히스토그램을 살펴본다.
# 1-11번 변수까지만 적용
par(mfrow=c(4,3))
for (x in names(wine[,1:11])){
if (is.numeric(wine[,x])){
hist(wine[,x],main = x,xlab = x,col="pink", border="white")
}
}
-> residual.sugar, chlorides 변수의 경우 사용하기에 적절해보이지 않는다.
2-3. 상관관계 분석
- 변수들 사이의 산점도 행렬을 살펴본다.
pairs(wine[1:11], col=c("orange", "skyblue"), pch=15)
- 변수들 사이의 상관 행렬을 살펴본다.
-> 선형적인 특징에 대해서만 알 수 있다.
-> 비선형적 특징에 대하여 관련이 있는 경우에는 상관계수에 나타나지 않는다.
install.packages("corrplot")
library(corrplot)M <- cor(wine)
corrplot(M, method = "number")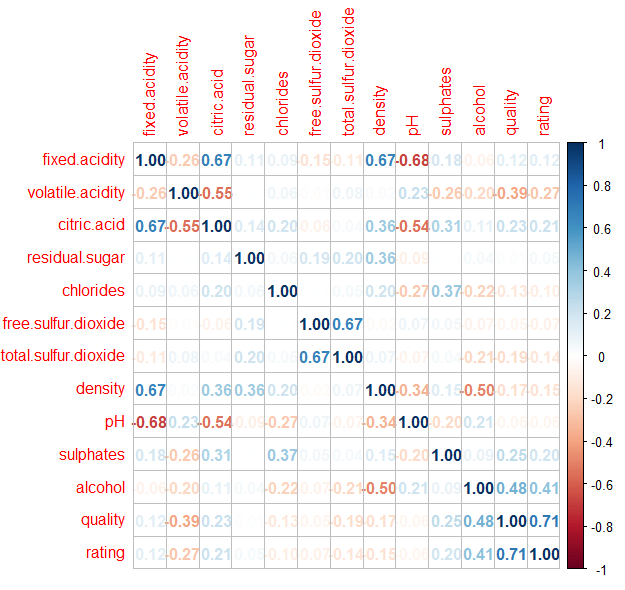
-> quality는 alcohol과 volatile.acidity와 어느정도 상관 관계를 갖는다.
3. 데이터 분할
- 필요한 패키지를 불러온다.
install.packages("caTools")
library(caTools)
- 전체 데이터 중 70%는 training data로, 나머지 30%는 testing data로 분리한다.
- 그러한 train, test data set을 20개를 생성한다.
- sample.split(Y, SplitRatio = 2/3, group = NULL) 함수는 Y 벡터의 크기에서 랜덤 번호에 대해 지정한 비율 만큼 TRUE를 나머지는 FALSE를 출력한다.
- 참고 : sample.split function - RDocumentation
# train : test = 7 : 3 -> 20 set
train<-vector("list", 20)
test<-vector("list", 20)
for(x in 1:20){
spl<-sample.split(wine$rating, 0.7)
train[[x]]<-subset(wine, spl==TRUE)
test[[x]]<-subset(wine, spl==FALSE)
}
- spl 변수를 한번 살펴보자.
summary(spl) Mode FALSE TRUE
logical 479 1120-> True의 개수가 1120개, False의 개수가 479개로 7:3의 비율이 잘 적용되어있다.
-> 전체 데이터 1599개에서 70%를 적용하면 사실 1119.3이 나오는 데 올림을 적용시키는 것 같다.
4. Bayes Classification
5. Logistic Regression
-> logistic regression의 경우 예측 변수(종속변수)가 이산화 변수여야한다.
5-1. Logistic Regression 적용
- 필요한 패키지를 불러온다.
install.packages("class")
library(class)
- 첫번째 train, test set에 대하여 logistic regression을 적용한다.
logit_model<-glm(rating ~ .-quality, data = train[[1]], family=binomial(link=logit))summary(logit_model)Call:
glm(formula = rating ~ . - quality, family = binomial(link = logit),
data = train[[1]])
Deviance Residuals:
Min 1Q Median 3Q Max
-2.1003 -0.4306 -0.2283 -0.1030 2.9424
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 88.37372 134.58759 0.657 0.511421
fixed.acidity 0.16798 0.16073 1.045 0.295997
volatile.acidity -2.42213 0.94827 -2.554 0.010641 *
citric.acid 0.12671 1.03078 0.123 0.902165
residual.sugar 0.13627 0.09877 1.380 0.167692
chlorides -9.84660 4.71532 -2.088 0.036779 *
free.sulfur.dioxide 0.02701 0.01614 1.673 0.094231 .
total.sulfur.dioxide -0.02853 0.00734 -3.887 0.000102 ***
density -101.66364 137.55110 -0.739 0.459848
pH -0.15909 1.23325 -0.129 0.897354
sulphates 3.89338 0.64226 6.062 1.34e-09 ***
alcohol 0.89155 0.16277 5.477 4.32e-08 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 889.23 on 1118 degrees of freedom
Residual deviance: 606.33 on 1107 degrees of freedom
AIC: 630.33
Number of Fisher Scoring iterations: 6
- 생성된 모델을 이용하여 예측을 해본다. (분류 기준값 : 0.5)
pred<-predict(logit_model, test[[1]], type="response") >= 0.5
- 어떻게 예측을 하였는지 테이블로 만들어서 살펴본다.
tab<-table(pred, test[[1]][["rating"]])
tabpred 0 1
FALSE 404 49
TRUE 11 16
- 정확도를 계산하였더니 0.875가 나왔다.
accuracy<-sum(tab[1,1], tab[2,2]) / sum(tab)
accuracy
[1] 0.875
- 오류율은 0.12가 나왔다.
1-accuracy
[1] 0.125
5-2. 변수선택 (Stepwise)
- step() 함수를 이용하여 부적절한 변수들을 제거한다.
- AIC가 더 이상 작아지지 않는 모델을 찾아낸다.
reduce_model<-step(logit_model)Start: AIC=630.33
rating ~ (fixed.acidity + volatile.acidity + citric.acid + residual.sugar +
chlorides + free.sulfur.dioxide + total.sulfur.dioxide +
density + pH + sulphates + alcohol + quality) - quality
Df Deviance AIC
- citric.acid 1 606.34 628.34
- pH 1 606.34 628.34
- density 1 606.87 628.87
- fixed.acidity 1 607.41 629.41
- residual.sugar 1 608.04 630.04
<none> 606.33 630.33
- free.sulfur.dioxide 1 609.15 631.15
- chlorides 1 613.27 635.27
- volatile.acidity 1 613.29 635.29
- total.sulfur.dioxide 1 624.85 646.85
- alcohol 1 638.23 660.23
- sulphates 1 639.19 661.19
Step: AIC=628.34
rating ~ fixed.acidity + volatile.acidity + residual.sugar +
chlorides + free.sulfur.dioxide + total.sulfur.dioxide +
density + pH + sulphates + alcohol
Df Deviance AIC
- pH 1 606.36 626.36
- density 1 606.87 626.87
- fixed.acidity 1 607.62 627.62
- residual.sugar 1 608.07 628.07
<none> 606.34 628.34
- free.sulfur.dioxide 1 609.15 629.15
- chlorides 1 613.64 633.64
- volatile.acidity 1 617.57 637.57
- total.sulfur.dioxide 1 624.97 644.97
- sulphates 1 639.19 659.19
- alcohol 1 640.08 660.08
Step: AIC=626.36
rating ~ fixed.acidity + volatile.acidity + residual.sugar +
chlorides + free.sulfur.dioxide + total.sulfur.dioxide +
density + sulphates + alcohol
Df Deviance AIC
- density 1 607.31 625.31
<none> 606.36 626.36
- residual.sugar 1 608.41 626.41
- free.sulfur.dioxide 1 609.16 627.16
- fixed.acidity 1 610.19 628.19
- chlorides 1 614.19 632.19
- volatile.acidity 1 617.72 635.72
- total.sulfur.dioxide 1 625.55 643.55
- sulphates 1 639.43 657.43
- alcohol 1 649.93 667.93
Step: AIC=625.31
rating ~ fixed.acidity + volatile.acidity + residual.sugar +
chlorides + free.sulfur.dioxide + total.sulfur.dioxide +
sulphates + alcohol
Df Deviance AIC
- residual.sugar 1 608.46 624.46
<none> 607.31 625.31
- free.sulfur.dioxide 1 610.36 626.36
- fixed.acidity 1 610.96 626.96
- chlorides 1 615.75 631.75
- volatile.acidity 1 622.03 638.03
- total.sulfur.dioxide 1 626.71 642.71
- sulphates 1 639.66 655.66
- alcohol 1 707.03 723.03
Step: AIC=624.46
rating ~ fixed.acidity + volatile.acidity + chlorides + free.sulfur.dioxide +
total.sulfur.dioxide + sulphates + alcohol
Df Deviance AIC
<none> 608.46 624.46
- free.sulfur.dioxide 1 611.10 625.10
- fixed.acidity 1 612.92 626.92
- chlorides 1 616.26 630.26
- volatile.acidity 1 622.86 636.86
- total.sulfur.dioxide 1 626.84 640.84
- sulphates 1 640.23 654.23
- alcohol 1 712.42 726.42
- 부적절한 변수들을 제거한 모델의 정보를 살펴본다.
summary(reduce_model)Call:
glm(formula = rating ~ fixed.acidity + volatile.acidity + chlorides +
free.sulfur.dioxide + total.sulfur.dioxide + sulphates +
alcohol, family = binomial(link = logit), data = train[[1]])
Deviance Residuals:
Min 1Q Median 3Q Max
-2.1273 -0.4346 -0.2278 -0.1012 2.9627
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -13.518457 1.625004 -8.319 < 2e-16 ***
fixed.acidity 0.127019 0.059746 2.126 0.033503 *
volatile.acidity -2.676413 0.732856 -3.652 0.000260 ***
chlorides -9.807867 4.626299 -2.120 0.034004 *
free.sulfur.dioxide 0.025660 0.015841 1.620 0.105266
total.sulfur.dioxide -0.027860 0.007248 -3.844 0.000121 ***
sulphates 3.725392 0.626808 5.943 2.79e-09 ***
alcohol 0.985791 0.105867 9.312 < 2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 889.23 on 1118 degrees of freedom
Residual deviance: 608.46 on 1111 degrees of freedom
AIC: 624.46
Number of Fisher Scoring iterations: 6-> AIC 값이 630.33에서 624.46로 줄어들었다.
-> 변수가 11개에서 7개로 줄어들었다.
-> citric.acid, residual.sugar, density, pH, 총 4개의 변수가 제거되었다.
-> fixed.acidity, residual.sugar, density 변수가 적절하지 않을 것이라고 생각했는데, 조금 다른 결과가 나왔다.
- 수정한 모델을 이용하여 예측을 진행한다. (분류 기준값 : 0.5)
> pred<-predict(reduce_model, test[[1]], type="response") >= 0.5
> tab<-table(pred, test[[1]][["rating"]])
> tab
pred 0 1
FALSE 404 49
TRUE 11 16
> accuracy<-sum(tab[1,1], tab[2,2]) / sum(tab)
> accuracy
[1] 0.875-> 정확도가 바뀌진 않았다....
5-3. 여러 train, test set에 Logistic Regression 적용
- 만들어 놓은 20개의 trian, test set에 대하여 logistic regression을 적용하고 예측해본다. (분류 기준값 : 0.5)
- fixed.acidity, residual.sugar, density 변수를 제거하여 모델을 생성한다.
acc_glm0.5<-c()
for (x in 1:20){
logit.model<-glm(rating ~ .-quality-citric.acid-residual.sugar-density-pH, data = train[[x]], family=binomial(link=logit))
pred<-(predict(logit.model, test[[x]], type="response") >= 0.5)
tab <- table(pred,test[[x]][["rating"]])
acc_glm0.5<-c(acc_glm0.5, sum(tab[1,1], tab[2,2]) / sum(tab))
}
- 평균 정확도는 0.874375가 나왔다.
mean(acc_glm0.5)
[1] 0.874375
- 정확도의 표준편차는 0.0103639이 나왔다.
> sd(acc_glm0.5)
[1] 0.0103639
5-4. 분류 기준값을 바꿔가면서 Logistic Regression 적용
- 분류 기준값을 0.3, 0.4, 0.5, 0.6, 0.7로 돌아가면서 적용해본다.
# 표준정확도, 표준편차 리스트
accuracy<-list()
# 분류 기준값
threshold<-c(0.3, 0.4, 0.5, 0.6, 0.7)
for(i in 1:5){
acc_glm<-c()
for(x in 1:20){
logit.model<-glm(rating ~ .-quality-citric.acid-residual.sugar-density-pH, data = train[[x]], family=binomial(link=logit))
pred<-(predict(logit.model, test[[x]], type="response") >= threshold[i])
tab <- table(pred,test[[x]][["rating"]])
acc_glm<-c(acc_glm, sum(tab[1,1], tab[2,2]) / sum(tab))
}
accuracy[[i]]<-c(mean(acc_glm), sd(acc_glm))
}
accuracy <- data.frame(Reduce(cbind, accuracy))
colnames(accuracy) <- c('0.3', '0.4', '0.5', '0.6', '0.7')
rownames(accuracy) <- c('mean', 'sd')
accuracy 0.3 0.4 0.5 0.6 0.7
mean 0.85635417 0.86822917 0.8743750 0.87750000 0.869687500
sd 0.01431417 0.01158719 0.0103639 0.00595426 0.005256358-> 분류 기준값이 0.6일 때의 표준 정확도가 가장 높은 것을 알 수 있다.
- 표준 정확도와 표준편차를 이용하여 95% 신뢰구간 그래프를 그려본다.
- 점 : 표준 정확도(Mean) / 세로 선 : 95% 신뢰구간(CI)
accuracy <- t(accuracy)
plot(1:5, accuracy[,1], pch = 16, lty = 1, type = 'o',
xlim = c(0.5, 6), ylim = c(0.5, 0.9),
ylab = 'Mean & CI', xlab = 'Threshold', axes = F)
axis(1, at = 1:5, lab = c('0.3', '0.4', '0.5', '0.6', '0.7'))
axis(2, ylim = c(0.7, 1))
arrows(1:5, accuracy[,1] - 1.96 * accuracy[,2],
1:5, accuracy[,1] + 1.96 * accuracy[,2],
code = 3, angle = 90, length = 0.05)
6. Decission Tree
-> 질적 데이터에 특화된 분석 기법이다.
-> 양적 데이터의 경우 범주형으로 변환하여 decision tree에 적용할 수 있다.
-> 사람들이 직관적으로 이해하기 쉬운 분석 방법이다.
6-1. 연속형 변수의 범주화
- 현재 우리의 데이터의 모든 변수는 연속형 데이터이다. 따라서 이 변수들을 모두 범주형 데이터로 변환해주어야 한다.
-> 중간값에 대한 지니계수를 구하여 가장 적절한 구분 경계값을 구할 수도 있지만 현재 어떻게 적용시켜야힐지 모르겠어서 변수별로 rating로 그룹화하여 박스플롯을 그리고 이것을 관찰해 구분 경계값을 구해보려고한다.
- rating변수에 대한 각각의 변수값들의 분포를 박스 플롯으로 나타내본다.
p1 <- ggplot(wine, aes(as.factor(rating),fixed.acidity))+ geom_boxplot() + coord_cartesian(ylim = c(min(wine$fixed.acidity),max(wine$fixed.acidity)))
p2 <- ggplot(wine, aes(as.factor(rating),volatile.acidity))+ geom_boxplot()+ coord_cartesian(ylim = c(min(wine$volatile.acidity), max(wine$volatile.acidity)))
p5 <- ggplot(wine, aes(as.factor(rating),chlorides))+ geom_boxplot()+ coord_cartesian(ylim = c(min(wine$chlorides), max(wine$chlorides)))
p6 <- ggplot(wine, aes(as.factor(rating),free.sulfur.dioxide))+ geom_boxplot()+ coord_cartesian(ylim = c(min(wine$free.sulfur.dioxide), max(wine$free.sulfur.dioxide)))
p7 <- ggplot(wine, aes(as.factor(rating),total.sulfur.dioxide))+ geom_boxplot()+ coord_cartesian(ylim = c(min(wine$total.sulfur.dioxide), max(wine$total.sulfur.dioxide)))
p10 <- ggplot(wine, aes(as.factor(rating),sulphates))+ geom_boxplot()+ coord_cartesian(ylim = c(min(wine$sulphates), max(wine$sulphates)))
p11 <- ggplot(wine, aes(as.factor(rating),alcohol))+ geom_boxplot()+ coord_cartesian(ylim = c(min(wine$alcohol), max(wine$alcohol)))
grid.arrange(p1, p2, p5, p6, p7, p10, p11, nrow=2)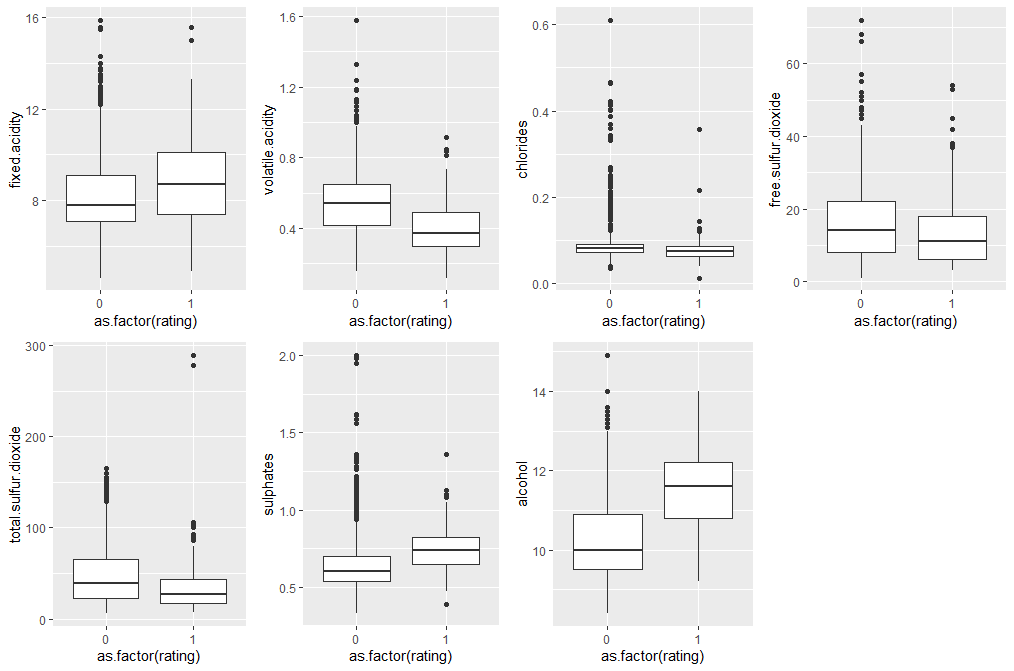
-> fixed.acidity : 8.5, volatile.acidity : 0.5, free.sulfur.dioxide : 12, total.sulfur.dioxide : 40, sulphates : 0.7, alcohol : 11
-> chlorides 변수의 경우 박스 플롯만으로는 판단이 어려워 평균 값인 0.08747을 경계값으로 한다.
- 각 변수를 결정한 구분 경계값을 이용하여 범주화 한다.
# 범주화한 데이터 저장
wine_dt<-wine
# 각 변수 범주화
wine_dt<-within(wine_dt, {
fa = character(0)
fa[fixed.acidity <= 8.5] = "low"
fa[fixed.acidity > 8.5] = "high"
fa = factor(fa, level = c("low", "high"))
})
wine_dt<-within(wine_dt, {
va = character(0)
va[volatile.acidity <= 0.5] = "low"
va[volatile.acidity > 0.5] = "high"
va = factor(va, level = c("low", "high"))
})
wine_dt<-within(wine_dt, {
c = character(0)
c[chlorides <= 0.08747] = "low"
c[chlorides > 0.08747] = "high"
c = factor(c, level = c("low", "high"))
})
wine_dt<-within(wine_dt, {
fsd = character(0)
fsd[free.sulfur.dioxide <= 12] = "low"
fsd[free.sulfur.dioxide > 12] = "high"
fsd = factor(fsd, level = c("low", "high"))
})
wine_dt<-within(wine_dt, {
tsd = character(0)
tsd[total.sulfur.dioxide <= 40] = "low"
tsd[total.sulfur.dioxide > 40] = "high"
tsd = factor(tsd, level = c("low", "high"))
})
wine_dt<-within(wine_dt, {
s = character(0)
s[sulphates <= 0.7] = "low"
s[sulphates > 0.7] = "high"
s = factor(s, level = c("low", "high"))
})
wine_dt<-within(wine_dt, {
a = character(0)
a[alcohol <= 11] = "low"
a[alcohol > 11] = "high"
a = factor(a, level = c("low", "high"))
})
wine_dt<-transform(wine_dt, rating = as.factor(rating))
# 필요없는 변수 제거
wine_dt<-wine_dt[13:20]str(wine_dt)'data.frame': 1599 obs. of 8 variables:
$ rating: num 0 0 0 0 0 0 0 1 1 0 ...
$ fa : Factor w/ 2 levels "low","high": 1 1 1 2 1 1 1 1 1 1 ...
$ va : Factor w/ 2 levels "low","high": 2 2 2 1 2 2 2 2 2 1 ...
$ c : Factor w/ 2 levels "low","high": 1 2 2 1 1 1 1 1 1 1 ...
$ fsd : Factor w/ 2 levels "low","high": 1 2 2 2 1 2 2 2 1 2 ...
$ tsd : Factor w/ 2 levels "low","high": 1 2 2 2 1 1 2 1 1 2 ...
$ s : Factor w/ 2 levels "low","high": 1 1 1 1 1 1 1 1 1 2 ...
$ a : Factor w/ 2 levels "low","high": 1 1 1 1 1 1 1 1 1 1 ...-> 모든 변수들이 범주형 데이터로 변화한 모습을 확인할 수 있다.
6-2. 데이터 분할
- 전체 데이터 중 70%는 training data로, 나머지 30%는 testing data로 분리한다. (20 set 생성)
# train : test = 7 : 3 -> 20 set
train_dt<-vector("list", 20)
test_dt<-vector("list", 20)
for(x in 1:20){
spl<-sample.split(wine_dt$rating, 0.7)
train_dt[[x]]<-subset(wine_dt, spl==TRUE)
test_dt[[x]]<-subset(wine_dt, spl==FALSE)
}
6-3. Decission Tree 적용
- 필요한 패키지를 불러온다.
install.packages("rpart")
library(rpart)
- 첫번째 train, test set에 대하여 decission tree를 적용한다. (최소가지치기 데이터 수 : 20)
tree_model<-rpart(rating~., data=train_dt[[1]])tree_modeln= 1119
node), split, n, loss, yval, (yprob)
* denotes terminal node
1) root 1119 152 0 (0.86416443 0.13583557)
2) a=low 833 51 0 (0.93877551 0.06122449) *
3) a=high 286 101 0 (0.64685315 0.35314685)
6) s=low 173 40 0 (0.76878613 0.23121387) *
7) s=high 113 52 1 (0.46017699 0.53982301)
14) va=high 31 11 0 (0.64516129 0.35483871) *
15) va=low 82 32 1 (0.39024390 0.60975610)
30) c=high 15 5 0 (0.66666667 0.33333333) *
31) c=low 67 22 1 (0.32835821 0.67164179) *-> 생성된 decission tree model의 모양을 알 수 있다.
- 생성된 decission tree model의 정보를 살펴볼 수 있다.
summary(tree_model)Call:
rpart(formula = rating ~ ., data = train_dt[[1]])
n= 1119
CP nsplit rel error xerror xstd
1 0.03947368 0 1.0000000 1.0000000 0.07540088
2 0.03289474 3 0.8815789 1.0197368 0.07602313
3 0.01000000 4 0.8486842 0.8618421 0.07075473
Variable importance
a s va c
66 24 5 5
Node number 1: 1119 observations, complexity param=0.03947368
predicted class=0 expected loss=0.1358356 P(node) =1
class counts: 967 152
probabilities: 0.864 0.136
left son=2 (833 obs) right son=3 (286 obs)
Primary splits:
a splits as LR, improve=36.286550, (0 missing)
s splits as LR, improve=20.078630, (0 missing)
va splits as RL, improve=13.401980, (0 missing)
tsd splits as RL, improve= 4.975030, (0 missing)
fa splits as LR, improve= 4.508321, (0 missing)
Node number 2: 833 observations
predicted class=0 expected loss=0.06122449 P(node) =0.7444147
class counts: 782 51
probabilities: 0.939 0.061
Node number 3: 286 observations, complexity param=0.03947368
predicted class=0 expected loss=0.3531469 P(node) =0.2555853
class counts: 185 101
probabilities: 0.647 0.353
left son=6 (173 obs) right son=7 (113 obs)
Primary splits:
s splits as LR, improve=13.0198500, (0 missing)
va splits as RL, improve= 8.1854110, (0 missing)
fa splits as LR, improve= 3.2730540, (0 missing)
fsd splits as RL, improve= 1.4288110, (0 missing)
c splits as RL, improve= 0.6217021, (0 missing)
Node number 6: 173 observations
predicted class=0 expected loss=0.2312139 P(node) =0.1546023
class counts: 133 40
probabilities: 0.769 0.231
Node number 7: 113 observations, complexity param=0.03947368
predicted class=1 expected loss=0.460177 P(node) =0.100983
class counts: 52 61
probabilities: 0.460 0.540
left son=14 (31 obs) right son=15 (82 obs)
Primary splits:
va splits as RL, improve=2.92365400, (0 missing)
c splits as RL, improve=2.53328200, (0 missing)
fsd splits as RL, improve=1.63701800, (0 missing)
tsd splits as RL, improve=0.72995050, (0 missing)
fa splits as LR, improve=0.01077531, (0 missing)
Node number 14: 31 observations
predicted class=0 expected loss=0.3548387 P(node) =0.02770331
class counts: 20 11
probabilities: 0.645 0.355
Node number 15: 82 observations, complexity param=0.03289474
predicted class=1 expected loss=0.3902439 P(node) =0.07327971
class counts: 32 50
probabilities: 0.390 0.610
left son=30 (15 obs) right son=31 (67 obs)
Primary splits:
c splits as RL, improve=2.80548500, (0 missing)
fsd splits as RL, improve=1.62342400, (0 missing)
tsd splits as RL, improve=0.24863270, (0 missing)
fa splits as RL, improve=0.09756098, (0 missing)
Node number 30: 15 observations
predicted class=0 expected loss=0.3333333 P(node) =0.01340483
class counts: 10 5
probabilities: 0.667 0.333
Node number 31: 67 observations
predicted class=1 expected loss=0.3283582 P(node) =0.05987489
class counts: 22 45
probabilities: 0.328 0.672
- plot()과 text()를 사용하여 decission tree model을 시각화 할 수 있다.
plot(tree_model, compress=T, uniform=T, margin=0.1)
text(tree_model, use.n=T, col="blue")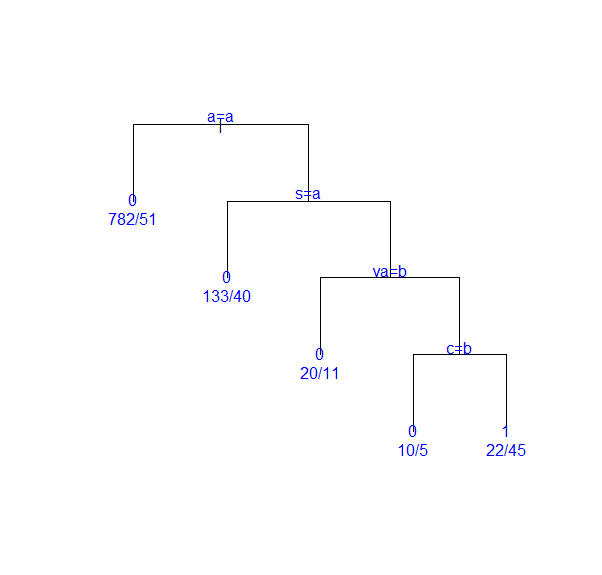
-> a=a는 좌측 가지의 조건이며 a는 첫번째 변수값 "low"를 의미한다.
-> terminal node의 0, 1은 rating의 값이며 1은 "Good"을 의미한다.
-> 따라서, alcohol이 높고, sulphates가 높고, volatile.acidity가 낮고, chlorides가 낮으면 그 와인은 괜찮은 와인이라고 분류할 수 있다.
-> 다른 시각화 방법도 적용해보기
- 생성된 decission tree model을 적용하여 예측을 해본다.
pred<-predict(tree_model, newdata=test_dt[[1]], type="class")
tab<-table(pred, test[[1]][["rating"]])
tab
pred 0 1
0 393 60
1 22 5
accuracy<-sumaccuracy<-sum(tab[1,1], tab[2,2]) / sum(tab)
accuracy
[1] 0.8291667-> 0.8291667의 정확도를 보인다.
6-4. 다양한 방법으로 Decission Tree 적용
- 여러 train, test set에 최소가지치기 데이터 수를 바꿔가면서 decission tree를 적용해본다.
- 최소가지치기 데이터 수를 1, 5, 10, 20, 30로 돌아가면서 적용해본다.
# 표준정확도, 표준편차 리스트
accuracy<-list()
# 분류 기준값
threshold<-c(1, 5, 10, 20, 30)
for(i in 1:5){
acc_dt<-c()
for(x in 1:20){
tree_model<-rpart(rating~., data=train_dt[[x]], control=rpart.control(minsplit=threshold[i]))
pred<-predict(tree_model, newdata=test_dt[[x]], type="class")
tab<-table(pred, test_dt[[x]][["rating"]])
acc_dt<-c(acc_dt, sum(tab[1,1], tab[2,2]) / sum(tab))
}
accuracy[[i]]<-c(mean(acc_dt), sd(acc_dt))
}
accuracy <- data.frame(Reduce(cbind, accuracy))
colnames(accuracy) <- c('1', '2', '5', '10', '20')
rownames(accuracy) <- c('mean', 'sd')
accuracy 1 2 5 10 20
mean 0.869791667 0.869791667 0.869791667 0.870729167 0.870729167
sd 0.006843195 0.006843195 0.006843195 0.007136507 0.007136507-> 최소가지치기 데이터수가 늘어날 수록 평균 정확도는 높아지지만 표준편차가 늘어나는 것을 볼 수 있다.
- 최소가지치기 데이터수를 더 늘려서 분석해보았다.
# 표준정확도, 표준편차 리스트
accuracy<-list()
# 분류 기준값
threshold<-c(50, 75, 100, 150, 200)
for(i in 1:5){
acc_dt<-c()
for(x in 1:20){
tree_model<-rpart(rating~., data=train_dt[[x]], control=rpart.control(minsplit=threshold[i]))
pred<-predict(tree_model, newdata=test_dt[[x]], type="class")
tab<-table(pred, test_dt[[x]][["rating"]])
acc_dt<-c(acc_dt, sum(tab[1,1], tab[2,2]) / sum(tab))
}
accuracy[[i]]<-c(mean(acc_dt), sd(acc_dt))
}
accuracy <- data.frame(Reduce(cbind, accuracy))
colnames(accuracy) <- c('50', '75', '100', '150', '200')
rownames(accuracy) <- c('mean', 'sd')
accuracy 50 75 100 150 200
mean 0.870312500 0.871875000 0.874375000 0.859375000 0.860312500
sd 0.008652733 0.009230737 0.009294857 0.006064499 0.005256358-> 최소 가지치기 데이터수가 100개일 때 유독 높은 평균 정확도를 보임을 알 수 있다.
- 표준 정확도와 표준편차를 이용하여 95% 신뢰구간 그래프를 그려본다.
- 점 : 표준 정확도(Mean) / 세로 선 : 95% 신뢰구간(CI)
accuracy <- t(accuracy)
plot(1:5, accuracy[,1], pch = 16, lty = 1, type = 'o',
ylim=c(0.5, 0.9), ylab = 'Mean & CI', xlab = 'Threshold', axes = F)
axis(1, at = 1:5, lab = c('50', '75', '100', '150', '200'))
axis(2, ylim = c(0.7, 1))
arrows(1:5, accuracy[,1] - 1.96 * accuracy[,2],
1:5, accuracy[,1] + 1.96 * accuracy[,2],
code = 3, angle = 90, length = 0.05)
7. 분석 모델 평가 및 비교
7-1. 평균 정확도와 표준편차 비교
- logistic regresson과 decission tree의 평균 정확도와 표준편차를 비교하여 표로 정리하였다.

-> logistic regression model의 분류기준값을 0.6으로 하여 적용하였을 때 가장 높은 정확도를 보인다.
-> 원본 데이터의 변수가 모두 연속형 변수이기 때문에 decision tree보다 logistic regression으로 분석하였을 때 더 높은 정확도가 나온 것 같다.
-> decision tree에 사용하기 위해 연속형 변수들을 범주형 데이터로 변환할 때 다른 좋은 방법을 쓰면 정확도가 올라갈 것 같다.
7-2. ROC (Receiver Operating Characteristic) & Lift Chart
- 참고 : [ADP] R을 활용한 모형평가 방법(2) - Confusion matrix, ROC Curve, Gain chart (tistory.com)
ref.
- R, SAS, MS-SQL을 활용한 데이터마이닝, 이정진
- Predicting White Wine Quality | Kaggle
'Data > R' 카테고리의 다른 글
| [데이터사이언스/R] Red Wine Quality -아다부스팅 앙상블 ( AdaBoosting Ensemble) (0) | 2021.07.14 |
|---|---|
| [데이터사이언스/R] Red Wine Quality - 서포트 벡터 머신 (Support Vector Machine, 지지 벡터 머신) (0) | 2021.07.13 |
| [데이터 분석해보기] Bayes Classification (베이즈 분류) (feat. Mushroom) (1) | 2021.07.07 |
| [빅데이터] 분류분석 (Classification Analysis) (0) | 2021.07.07 |
| Linear Regression (선형 회귀) (0) | 2021.07.06 |
